早教吧作业答案频道 -->数学-->
在△ABC中,CD⊥AB于点D,∠A=2∠BCD.(1)如图1,求证:AB=AC;(2)如图2,E是AB上一点,F是AC延长线上一点,连接CE、BF,CE=BF,求证:∠BEC=∠CFB;(3)如图3,在(2)的条件下,作EG∥BC交AC
题目详情
在△ABC中,CD⊥AB于点D,∠A=2∠BCD.
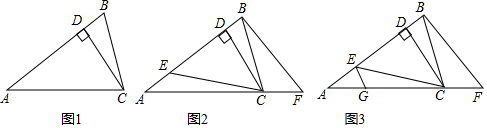
(1)如图1,求证:AB=AC;
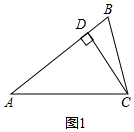
(2)如图2,E是AB上一点,F是AC延长线上一点,连接CE、BF,CE=BF,求证:∠BEC=∠CFB;
(3)如图3,在(2)的条件下,作EG∥BC交AC于点G,若∠CBF=2∠ACE,EG=2,BC=6,求BF的长.

(1)如图1,求证:AB=AC;
(2)如图2,E是AB上一点,F是AC延长线上一点,连接CE、BF,CE=BF,求证:∠BEC=∠CFB;
(3)如图3,在(2)的条件下,作EG∥BC交AC于点G,若∠CBF=2∠ACE,EG=2,BC=6,求BF的长.
▼优质解答
答案和解析
 (1)如图1,设∠BCD=x,则∠A=2∠BCD=2x,
(1)如图1,设∠BCD=x,则∠A=2∠BCD=2x,
∵CD⊥AB,
∴∠CDB=90°,
∴∠ABC=90°-x,
∵∠A=2x,
∴∠ACB=180°-2x-(90°-x)=90°-x,
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:如图2,作BH⊥AC于H,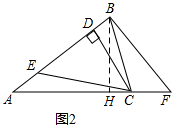
∴∠AHB=∠ADC=90°,
∵在∴△ABH和△ACD中,
,
∴△ABH≌△ACD(AAS),
∴BH=CD,
∵∠BHF=∠EDC=90°,
∴在Rt△BHF和Rt△CDE中,
,
∴Rt△BHF≌Rt△CDE(HL),
∴∠BEC=∠CFB;
(3)如图3,延长CB至点M,使BM=EG,连接EM,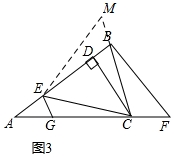
设∠ACE=α,∠CFB=β,
∴∠CBF=2∠ACE=2α,∠ACB=∠ABC=2α+β,∠BEC=∠CFB=β,
∵∠ACE=α,
∴∠ECB=α+β,
在△ECB中,α+β+β+2α+β=180°,
∴α+β=60°,
∴∠ECB=60°,
∵EG∥BC,
∴∠AEG=∠ABC,∠AGE=∠ACB,
∵∠ABC=∠ACB,
∴∠AEG=∠ABC=∠ACB=∠AGE,
∴AE=AG,
∵AB=AC,
∴AB-AE=AC-AG,
∴BE=CG,
∵∠AGE+∠EGC=180°,∠ABC+∠EBM=180°,
又∵∠AGE=∠ABC,
∴∠EGC=∠EBM,
∵BM=EG,
∴△EGC≌△MBE(SAS),
∴EM=EC,
∵∠ECB=60°,
∴△ECM是等边三角形,
∴CE=CM=BM+BC=EG+BC=2+6=8,
又∵CE=BF,
∴BF=8.
 (1)如图1,设∠BCD=x,则∠A=2∠BCD=2x,
(1)如图1,设∠BCD=x,则∠A=2∠BCD=2x,∵CD⊥AB,
∴∠CDB=90°,
∴∠ABC=90°-x,
∵∠A=2x,
∴∠ACB=180°-2x-(90°-x)=90°-x,
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:如图2,作BH⊥AC于H,

∴∠AHB=∠ADC=90°,
∵在∴△ABH和△ACD中,
|
∴△ABH≌△ACD(AAS),
∴BH=CD,
∵∠BHF=∠EDC=90°,
∴在Rt△BHF和Rt△CDE中,
|
∴Rt△BHF≌Rt△CDE(HL),
∴∠BEC=∠CFB;
(3)如图3,延长CB至点M,使BM=EG,连接EM,

设∠ACE=α,∠CFB=β,
∴∠CBF=2∠ACE=2α,∠ACB=∠ABC=2α+β,∠BEC=∠CFB=β,
∵∠ACE=α,
∴∠ECB=α+β,
在△ECB中,α+β+β+2α+β=180°,
∴α+β=60°,
∴∠ECB=60°,
∵EG∥BC,
∴∠AEG=∠ABC,∠AGE=∠ACB,
∵∠ABC=∠ACB,
∴∠AEG=∠ABC=∠ACB=∠AGE,
∴AE=AG,
∵AB=AC,
∴AB-AE=AC-AG,
∴BE=CG,
∵∠AGE+∠EGC=180°,∠ABC+∠EBM=180°,
又∵∠AGE=∠ABC,
∴∠EGC=∠EBM,
∵BM=EG,
∴△EGC≌△MBE(SAS),
∴EM=EC,
∵∠ECB=60°,
∴△ECM是等边三角形,
∴CE=CM=BM+BC=EG+BC=2+6=8,
又∵CE=BF,
∴BF=8.
看了在△ABC中,CD⊥AB于点D...的网友还看了以下:
如图所示,读句画图:①连接BD、AD;②画直线AB、CD相交于点E;③延长线段BC与线段蹦的反向延 2020-07-04 …
如图,AB是O的直径,C是弧AB的中点,连接AC并延长至D,使DC=CA,连接DB,点E为OB的中 2020-07-21 …
如图,已知矩形ABCD(AB<AD).(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;①以点A为 2020-07-22 …
(2014•道外区三模)如图,在正方形ABCD中,点P为AD边上一点,PC的垂直平分线交PC于E交 2020-07-29 …
如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.(1)求证:B 2020-08-01 …
(2014•东营)如图,四边形ABCD为菱形,AB=BD,点B、C、D、G四个点在同一个圆⊙O上,连 2020-11-03 …
如图,点A、B、C在同一条直线上,分别以AB、BC为边向外作等边三角形ABD、BCE,AE交BD于F 2020-11-03 …
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作 2020-11-03 …
如图①,已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF 2020-11-27 …
如图,已知四边形AEBC,对角线AB,CE为O的直径,以BC为直径的圆与AB交与点D,连接CD,过点 2020-12-25 …