已知函数f(x)=ex,x≤-1xe,x>-1,关于x的方程f2(x)+t|f(x)|+1=0(t∈R)有四个不同的实数根,则t的取值范围为()A.(-∞,-e2+1e)B.(e2+1e,+∞)C.(-e2+1e,-2)D.(2,e2+1e)
已知函数f(x)=
,关于x的方程f2(x)+t|f(x)|+1=0(t∈R)有四个不同的实数根,则t的取值范围为( )ex,x≤-1
,x>-1x e
A. (-∞,-
)e2+1 e
B. (
,+∞)e2+1 e
C. (-
,-2)e2+1 e
D. (2,
)e2+1 e
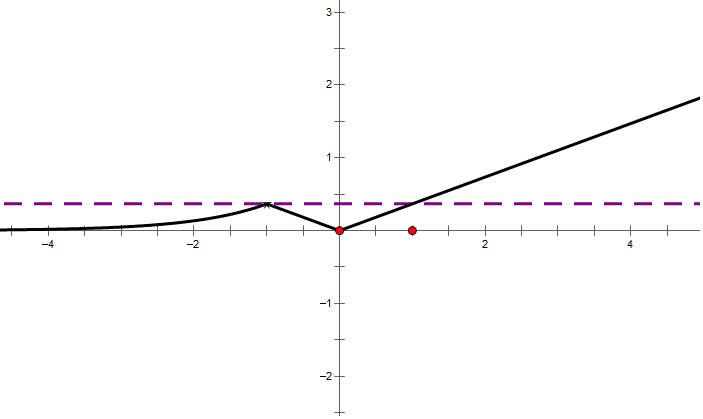
|f(x)|=
|
令|f(x)|=m,由y=|f(x)|的图象可知:
当m=0,或m>
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
故方程f2(x)+t|f(x)|+1=0有四个不同的实数根,则|f(x)|的两个值必须一个在(0,
| 1 |
| e |
| 1 |
| e |
即方程m2+tm+1=0有两个不等的实根m1,m2,且m1∈(0,
| 1 |
| e |
| 1 |
| e |
令g(m)=m2+tm+1
∵g(0)=1>0
∴只需g(
| 1 |
| e |
| 1 |
| e2 |
| t |
| e |
| e2+1 |
| e |
即t的取值范围为(-∞,-
| e2+1 |
| e |
已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=(1e)x+2,x≤-1f(x-1),-1 2020-05-13 …
已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=(1e)x+2,x≤-1f(x-1),-1 2020-07-14 …
(2014•绵阳三模)已知f(x)=|x|ex(x∈R),若关于x的方程f2(x)-tf(x)+t 2020-07-21 …
已知函数f(x)=lnxx-kx(k∈R),在区间[1e,e2]上的有两个零点,则k的取值范围. 2020-07-26 …
设函数f(x)=x2-2ex-lnxx+a(其中e为自然对数的底数,若函数f(x)至少存在一个零点 2020-08-02 …
1+e2+e3+...+en=?1e平方+...+e的n次方 2020-10-31 …
已知函数f(x)=kx,g(x)=2lnx+2e(1e≤x≤e2),若f(x)与g(x)的图象上分别 2020-10-31 …
已知函数f(x)=ax-(2a+1)lnx-2x,g(x)=-2alnx-2x,其中a∈R(1)当a 2020-10-31 …
已知函数f(x)=x-alnx+a+bx.(1)若曲线y=f(x)在点(1,f(1))处的切线过点( 2020-10-31 …
若关于x的方程|ax-1|-2x=0有两个不相等的实数解,则实数a的取值范围是()A.(0,1e)∪ 2020-10-31 …