在平面直角坐标系xOy中，抛物线y=ax2+bx经过点A（-3，4），直线l与x轴相交于点B，与∠AOB的平分线相交于点C，直线l的解析式为y=kx-5k（k≠0），BC=OB．（1）若点C在此抛物线上，求抛物线的解析

Question

在平面直角坐标系xOy中，抛物线y=ax²+bx经过点A（-3，4），直线l与x轴相交于点B，与∠AOB的平分线相交于点C，直线l的解析式为y=kx-5k（k≠0），BC=OB．

（1）若点C在此抛物线上，求抛物线的解析式；
（2）在（1）的条件下，过点A作y轴的平行线，与直线l相交于点D，设P为抛物线上的一个动点，连接PA、PD，当S_△PAD=(2)/(3)S_△COB时，求点P的坐标．

Answer 1

（1）如图，A（-3，4），
∴OA=√(32+42)=5，
当y=0时，kx-5k=0，解得x=5，则B（5，0），
∵BC=BO=5，
∴∠BOC=∠BCO，
∵OC平分∠AOB，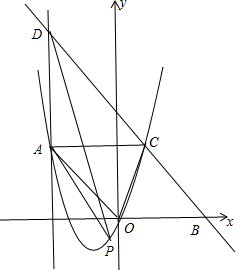
∴∠AOC=∠BOC，
∴∠AOC=∠BCO，
∴AO∥CB，
而OA=BC=5，
∴四边形AOBC为平行四边形，
∴AC∥OB，AC=OB=5，
∴C（2，4），
把A（-3，4），C（2，4）代入y=ax²+bx得

9a-3b=4

4a+2b=4

，解得a=(2)/(3)，b=(2)/(3)，
∴抛物线的解析式为y=(2)/(3)x²+(2)/(3)x；
（2）如图，把C（2，4）代入y=kx-5k得2k-5k=4，解得k=-(4)/(3)，
∴直线l的解析式为y=-(4)/(3)x+(20)/(3)，
当x=-2时，y=-(4)/(3)x+(20)/(3)=(32)/(3)，则D（-3，(32)/(3)），
∴AD=(32)/(3)-4=(20)/(3)，
设P（t，(2)/(3)t²+(2)/(3)t），
∵S_△PAD=(2)/(3)S_△COB，
∴(1)/(2)•(20)/(3)•|t+3|=(2)/(3)•(1)/(2)•5•4，解得t=-1或t=-5，
∴点P的坐标为（-1，0）或（-5，(40)/(3)）．