早教吧作业答案频道 -->数学-->
如图在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知AD=PD,PA=6,BC=8,DF=5,求证:(1)直线PA∥平面DEF;(2)平面DEF⊥平面ABC.
题目详情
如图在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点,已知AD=PD,PA=6,BC=8,DF=5,求证:
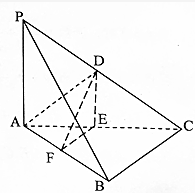
(1)直线PA∥平面DEF;
(2)平面DEF⊥平面ABC.

(1)直线PA∥平面DEF;
(2)平面DEF⊥平面ABC.
▼优质解答
答案和解析
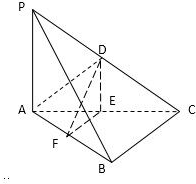 证明:(1)因为D,E是PC,AC中点,
证明:(1)因为D,E是PC,AC中点,
∴PA∥DE
∵DE⊂平面DEF,PA⊄平面DEF,
∴PA∥平面DEF;
(2)因为D,E,F分别为棱PC,AC,AB的中点,
∴PA=2DE,BC=2FE
∵PA=6,BC=8,DF=5
∴DE=3,EF=4,DF=5,
∴DE2+EF2=DF2∴DE⊥EF,
∵PD=AD,D为PC的中点
∴AD=DC
∵E为AC的中点,
∴DE⊥AC
∵AC∩EF=E,
∴DE⊥平面ABC,
∵DE⊂平面DEF,
∴平面DEF⊥平面ABC.
 证明:(1)因为D,E是PC,AC中点,
证明:(1)因为D,E是PC,AC中点,∴PA∥DE
∵DE⊂平面DEF,PA⊄平面DEF,
∴PA∥平面DEF;
(2)因为D,E,F分别为棱PC,AC,AB的中点,
∴PA=2DE,BC=2FE
∵PA=6,BC=8,DF=5
∴DE=3,EF=4,DF=5,
∴DE2+EF2=DF2∴DE⊥EF,
∵PD=AD,D为PC的中点
∴AD=DC
∵E为AC的中点,
∴DE⊥AC
∵AC∩EF=E,
∴DE⊥平面ABC,
∵DE⊂平面DEF,
∴平面DEF⊥平面ABC.
看了如图在三棱锥P-ABC中,D,...的网友还看了以下:
如图矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)求证:△ABE∽△DFA;(2)若AB= 2020-05-20 …
如图,四边形ABCD中,AD∥BC,∠A=90°,AB=AD=8,DE⊥DC交AB于E,DF平分∠ 2020-06-23 …
如图,在△ABC中,AB=8,BC=6,AC=10,D为边AC上一动点,DE⊥AB于点E,DF⊥B 2020-07-09 …
在直角三角形ABC中.角C等于90度,AC=8,CB=6,D是AB上任意一点,过点D作DE平行BC 2020-07-09 …
(1)如图,已知D是△ABC的边AB上一点,FC∥AB,DF交AC于点E,DE=EF.求证:E是A 2020-07-15 …
已知A、B、C不在同一直线上,顺次连接AB、BC、CA.(Ⅰ)如图①,点D在线段BC上,DE∥AB 2020-07-20 …
如图,已知△ABC中,AB=AC=5,tanC=3/4,BC=8,点D是BC边上一个动点(不与B、C 2020-11-01 …
如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方 2020-11-01 …
在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.(1)如图1,若D是BC边 2020-11-02 …
如图矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)求证:△ABE∽△DFA;(2)若AB=6 2020-11-03 …