早教吧作业答案频道 -->数学-->
如图1,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连接BE.(1)若AF是△ABE的中线,且AF=5,AE=6,连接DF,求DF的长;(2)若AF是△ABE的高,延长AF交BC于点G.①如图2,若点E是AC的中
题目详情
如图1,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E在AC边上,连接BE.
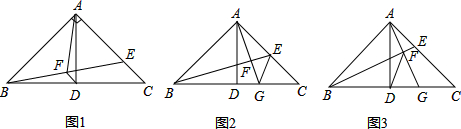
(1)若AF是△ABE的中线,且AF=5,AE=6,连接DF,求DF的长;
(2)若AF是△ABE的高,延长AF交BC于点G.
①如图2,若点E是AC的中点,连接EG,求证:AG+EG=BE;
②如图3,若点E是AC边上的动点,连接DF.当点E在AC边上(不含端点)运动时,∠DFG的大小是否改变,如果不变,请求出∠DFG的度数;如果要变,请说明理由.

(1)若AF是△ABE的中线,且AF=5,AE=6,连接DF,求DF的长;
(2)若AF是△ABE的高,延长AF交BC于点G.
①如图2,若点E是AC的中点,连接EG,求证:AG+EG=BE;
②如图3,若点E是AC边上的动点,连接DF.当点E在AC边上(不含端点)运动时,∠DFG的大小是否改变,如果不变,请求出∠DFG的度数;如果要变,请说明理由.
▼优质解答
答案和解析
(1)在Rt△ABE中,AF是中线,∴AF=12BE,∵AF=5,∴BE=10,在Rt△ABE中,AE=6,BE=10,可求得AB=8,又∵AB=AC,∴AC=8,∴CE=AC-AE=2,∵AB=AC,AD⊥BC,∴BD=DC,又∵点F是BE的中点,∴DF=12CE=1;(2)如图1,过...
看了如图1,△ABC中,∠BAC=...的网友还看了以下:
如图,已知,在平行四边形ABCD中,E是DC延长线上一点,连结AE交BC于点F.(1)若F是BC的 2020-05-13 …
如图,从矩形ABCD的一个顶点C向对角线BD作垂线CE,垂足是E.若BE=3DE两对角线的交点O至 2020-05-16 …
如图,从矩形ABCD中的一个顶点C向对角线BD做垂线CE,垂足是E,若BE=3DE,两对角线的交点 2020-05-16 …
如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于E,若OE:ED=1:3,AE=根号 2020-05-16 …
一个长方形长是a,宽是b,若长增加1/5,宽增加1/4,则面积增加多少?周长呢?弄清楚1/5和1/ 2020-06-04 …
在△ABC中,∠C=90°,AC=6cm,BC=8cm,扇形ODF与BC边相切,切点是E,若FO⊥ 2020-06-07 …
若规定E=的子集为E的第k个子集,其中k=,则(1)是E的第个子集;(2)E的第211个子集是若规 2020-06-11 …
已知椭圆E:x2a2+y2b2=1(b>a>0)的离心率为32,其中一个焦点F(3,0).(Ⅰ)求 2020-06-21 …
如图,△ABC中,AC>AB,D是BA延长线上一点,点E是∠CAD的平分线上一点,EB=EC,过点 2020-07-09 …
椭圆E:x2a2+y2b2=1(a>b>0)的左右焦点分别为F1,F2.(Ⅰ)若椭圆E的长轴长、短 2020-07-31 …