已知x1、x2是函数f（x）=13x2+12ax2+2bx（a，b∈R）的两个极值点，且x1∈（0，1），x2∈（1，2），则4a+3b的取值范围是（）A.（-9，-4）B.（-8，-4）C.（-9，-8）D.（-15，-4）

Question

已知x₁、x₂是函数f（x）=

(1)/(3)x²+(1)/(2)ax²+2bx（a，b∈R）的两个极值点，且x₁∈（0，1），x₂∈（1，2），则4a+3b的取值范围是（　　）

A. （-9，-4）

B. （-8，-4）

C. （-9，-8）

D. （-15，-4）

Answer 1

由题意，f′（x）=x²+ax+2b．
∵f（x）的两个极值点分别是x₁，x₂，x₁∈（0，1），
x₂∈（1，2），
∴

f′(0)=2b>0

f′(1)=1+a+2b<0

f′(2)=4+2a+2b>0

，
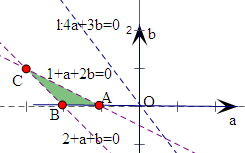
对应的平面区域如图所示，三个顶点坐标为A（-1，0），
B（-2，0），C（-3，1），则
在（-1，0）处，4a+3b=-4，在（-3，1）处，4a+3b=-9，
∴4a+3b的取值范围是（-9，-4）．
故选A．