早教吧作业答案频道 -->数学-->
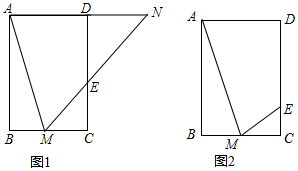
(1)如图1,矩形ABCD中,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E,请找出图1中的一个等腰三角形,并证明结论.(2)如图2,矩形ABCD中,AB=3,BC=2,点M为BC中点,连接AM
题目详情
(1)如图1,矩形ABCD中,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E,请找出图1中的一个等腰三角形,并证明结论.
(2)如图2,矩形ABCD中,AB=3,BC=2,点M为BC中点,连接AM,作∠AME=∠AMB,ME交CD于点E,求CE的长.
(2)如图2,矩形ABCD中,AB=3,BC=2,点M为BC中点,连接AM,作∠AME=∠AMB,ME交CD于点E,求CE的长.

▼优质解答
答案和解析
(1)△AMN是等腰三角形,
证明:∵四边形ABCD是矩形,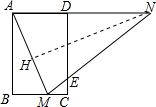
∴AD∥BC,
∴∠NAM=∠BMA,又∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)如图,作NH⊥AM于H,
∵AN=MN,NH⊥AM,
∴AH=
AM,
∵∠NHA=∠ABM=90°,∠AMN=∠AMB,
∴△NAH∽△AMB,
∴
=
,
∴AN•BM=AH•AM=
AM2,
∵M为BC中点,
∴BM=CM=
BC=1,
∵AM2=32+12=10,
∴AN=5,
∴DN=5-2=3,
设DE=x,则CE=3-x,
∵AN∥BC,
∴
=
,即
=
,
解得,x=
,即DE=
,
∴CE=
.
证明:∵四边形ABCD是矩形,

∴AD∥BC,
∴∠NAM=∠BMA,又∠AMN=∠AMB,
∴∠AMN=∠NAM,
∴AN=MN,即△AMN是等腰三角形;
(2)如图,作NH⊥AM于H,
∵AN=MN,NH⊥AM,
∴AH=
| 1 |
| 2 |
∵∠NHA=∠ABM=90°,∠AMN=∠AMB,
∴△NAH∽△AMB,
∴
| AN |
| AM |
| AH |
| BM |
∴AN•BM=AH•AM=
| 1 |
| 2 |
∵M为BC中点,
∴BM=CM=
| 1 |
| 2 |
∵AM2=32+12=10,
∴AN=5,
∴DN=5-2=3,
设DE=x,则CE=3-x,
∵AN∥BC,
∴
| DN |
| CM |
| DE |
| CE |
| 3 |
| 1 |
| x |
| 3-x |
解得,x=
| 9 |
| 4 |
| 9 |
| 4 |
∴CE=
| 3 |
| 4 |
看了 (1)如图1,矩形ABCD中...的网友还看了以下:
如图,已知,在平行四边形ABCD中,E是DC延长线上一点,连结AE交BC于点F.(1)若F是BC的 2020-05-13 …
如图,已知平行四边形ABCD,点P在对角线BD上,EF∥BC,GH∥AB,点E,H,F,G分别在边 2020-05-15 …
如图,已知在△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,使CE=BD,连结D 2020-05-17 …
如图,已知点B,C分别在∠A的两边上,连接BC,点P在∠A的内部,连接PB,PC.试探索∠BPC与 2020-06-13 …
如图,在三角形ABC中,点D是边BC的中点,点E在三角形ABC内,AE平分角BAC,CE⊥AE,点 2020-07-09 …
1.已知AB=CD,BC=CD,∠B=25°,求∠D的度数.(图1)ACBD2.已知,A,D,C, 2020-07-13 …
如图,菱形abcd中,点f是对角线bd上一点,连结af交bc于点e,连结cf.试猜想角aeb与角d 2020-07-30 …
(急)一道基本不等式证明题(高一数学)证明bc/a+ac/b+ab/c≥a+b+c证明:(请看我的 2020-08-03 …
如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E, 2020-08-03 …
如图,RT△ABC中,∠ABC=90°,以AB为直径的圆O交AC于点D,E是BC中点,连接DE、OE 2020-10-31 …