早教吧作业答案频道 -->数学-->
已知双曲线x2a2-y2b2=1的右顶点为A,O是坐标原点,以A为圆心的圆与渐近线交于P、Q两点,且∠PAQ=60°,OQ=3OP,求双曲线的离心率.
题目详情
已知双曲线
-
=1的右顶点为A,O是坐标原点,以A为圆心的圆与渐近线交于P、Q两点,且∠PAQ=60°,OQ=3OP,求双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
▼优质解答
答案和解析
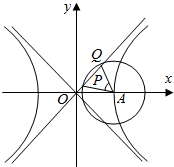 因为∠PAQ=60°且OQ=3OP,
因为∠PAQ=60°且OQ=3OP,
所以△QAP为等边三角形,
设AQ=2R,则OP=R,
渐近线方程为y=
x,A(a,0),取PQ的中点M,则AM=
由勾股定理可得(2R)2-R2=(
)2,
所以(ab)2=3R2(a2+b2)①
在△OQA中,
=
,所以7R2=a2②
①②结合c2=a2+b2,可得e=
=
.
 因为∠PAQ=60°且OQ=3OP,
因为∠PAQ=60°且OQ=3OP,所以△QAP为等边三角形,
设AQ=2R,则OP=R,
渐近线方程为y=
| b |
| a |
| |-ab| | ||
|
由勾股定理可得(2R)2-R2=(
| |-ab| | ||
|
所以(ab)2=3R2(a2+b2)①
在△OQA中,
| (3R)2+(2R)2-a2 |
| 2•3R•2R |
| 1 |
| 2 |
①②结合c2=a2+b2,可得e=
| c |
| a |
| ||
| 2 |
看了 已知双曲线x2a2-y2b2...的网友还看了以下:
如图,圆与坐标轴交于点.⑴求与直线垂直的圆的切线方程;⑵设点是圆上任意一点(不在坐标轴上),直线交 2020-06-15 …
过抛物线焦点的一条线与它交于两点P、Q,经过点P和抛物线顶点的直线交准线于点M求证直线MQ平行于抛 2020-06-16 …
如图,从点作x轴的垂线交曲线于点,曲线在点处的切线与x轴交于点P(2),再从作x轴的垂线交曲线于点 2020-07-22 …
如图,直线y=3x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,O 2020-07-24 …
如图,在正方形中,,将绕着点顺时针旋转(),得到,其中过点作与对角线垂直的直线交射线于点,射线与对 2020-07-25 …
(2014•荔城区二模)如图,直线y=x+1分别与x轴、y轴相交于点A、B,以点A为圆心,AB长为 2020-07-26 …
如图,直线y=x+1分别与x轴、y轴相交于点A、B,以点A为圆心,AB长为半径画弧交x轴于点A1, 2020-07-29 …
已知圆的方程为,直线过点,且与圆相切.(1)求直线的方程;(2)设圆与轴交于两点,是圆上异于的任意 2020-07-31 …
设抛物线C:x^2=2py,过焦点F的直线L交抛物线于点A,B,交准线于点E,过焦点F与L垂直的直 2020-07-31 …
如图,圆的直径,是延长线上一点,,割线交圆于点,,过点作的垂线,交直线于点,交直线于点.(1)求证: 2020-12-05 …