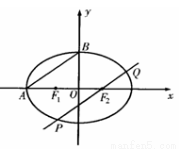
如图所示，、分别为椭圆：的左、右两个焦点，、为两个顶点，已知顶点到、两点的距离之和为.（1）求椭圆的方程；（2）求椭圆上任意一点到右焦点的距离的最

Question

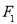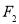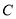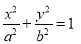
如图所示， 、 分别为椭圆 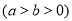： 的左、右两个焦点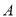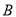， 、 为两个顶点，已知顶点 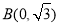到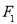 、 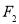两点的距离之和为 .

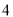（1）求椭圆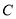 的方程；

（2）求椭圆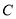 上任意一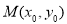点 到右焦点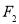 的距离的最小值；

（3）作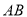 的平行线交椭圆 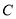于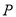 、 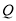两点，求弦长 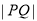的最大值，并求 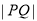取最大值时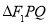 的面积.

 

 

Answer 1

（1）；（2）；（3），.【解析】试题分析：（1）求椭圆方程需遵循定型、定位、定量，这里结合椭圆定义不难求得方程；（2）首先写出表达式然后将关于的二元问题转化为关于的一元问题，归结为函数求最值，注意的隐含条件；（3）求直线被曲线截得的弦长是解析几何中的常见问题，求出弦长的表达式然后求最值，一般要关注判别式，否则易犯错.试题解析：（1）由已知得，∴椭圆的方程为 2分（2） ∵ 且，∴ 4分∴仅当为右顶点时 5分（3）设， ∵，∴可设直线的方程为：，代入，得 7分由韦达定理知：，， 9分又 ∴仅当时， 12分而此时点到直线：的距离，∴. 13分考点：1.椭圆方程与性质的互求；2.直线与椭圆的常规问题.