早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).(1)求线段AB的长;(2)若点E在线段AB上,OE⊥OF,OE=OF,求AE+AF的值;(3)在(2)的条件下,过点O作OM⊥
题目详情
如图,在平面直角坐标系中,点A在x轴上,且A(4,0),点B在y轴上,且B(0,4).
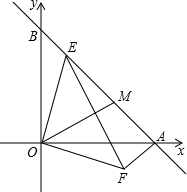
(1)求线段AB的长;
(2)若点E在线段AB上,OE⊥OF,OE=OF,求AE+AF的值;
(3)在(2)的条件下,过点O作OM⊥EF,交AB于点M,试确定线段BE、EM、AM的数量关系?并证明你的结论.

(1)求线段AB的长;
(2)若点E在线段AB上,OE⊥OF,OE=OF,求AE+AF的值;
(3)在(2)的条件下,过点O作OM⊥EF,交AB于点M,试确定线段BE、EM、AM的数量关系?并证明你的结论.
▼优质解答
答案和解析
(1)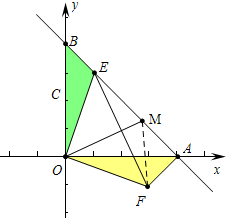 在RT△ABO中,∵AO=OB=4,
在RT△ABO中,∵AO=OB=4,
∴AB=
=
=4
.
(2)∵∠BOA=∠EOF=90°,
∴∠BOE=∠AOF,
在△BOE和△AOF中,
,
∴△BOE≌△AOF,
∴AF=BE,
∴AE+AF=AE+EB=AB=4
.
(3)结论:FM2=AM2+AF2,理由如下:
连接FM.∵OE=OF,OM⊥EF,
∴OM垂直平分分EF,
∴ME=MF,
∵OA=OB,∠AOB=90°,
∴∠OBA=∠OAB=45°
由(1)可知△BOE≌△AOF,
∴BE=AF,∠OBE=∠OAF=45°,
∴∠MAF=∠OAF+∠OAB=90°,
∴FM2=AM2+AF2,
∴EM2=BE2+AM2.
 在RT△ABO中,∵AO=OB=4,
在RT△ABO中,∵AO=OB=4,∴AB=
| AO2+OB2 |
| 42+42 |
| 2 |
(2)∵∠BOA=∠EOF=90°,
∴∠BOE=∠AOF,
在△BOE和△AOF中,
|
∴△BOE≌△AOF,
∴AF=BE,
∴AE+AF=AE+EB=AB=4
| 2 |
(3)结论:FM2=AM2+AF2,理由如下:
连接FM.∵OE=OF,OM⊥EF,
∴OM垂直平分分EF,
∴ME=MF,
∵OA=OB,∠AOB=90°,
∴∠OBA=∠OAB=45°
由(1)可知△BOE≌△AOF,
∴BE=AF,∠OBE=∠OAF=45°,
∴∠MAF=∠OAF+∠OAB=90°,
∴FM2=AM2+AF2,
∴EM2=BE2+AM2.
看了 如图,在平面直角坐标系中,点...的网友还看了以下:
如图,在正方形ABCD中,N是DC上的点,且DNNC=34,M是AD上异于D的点,且∠NMB=∠M 2020-04-07 …
已知如图,等腰Rt△ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA 2020-04-11 …
如图,在平行四边形ABCD中,E、F分别是AB、CD上的点,且EF∥BC,DE∥BF,则图共有个平 2020-05-13 …
如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC,AD上的 2020-05-13 …
如图,△ABC中,D、E是BC边上的点,且BD:DE:EC=3:2:1,P是AC边上的点,且AP: 2020-05-13 …
如图,点D、E分别是等边三角形ABC的BC、AC边上的点,且BD=CE,AD与BE相交于点F. ( 2020-05-13 …
如图,已知点F是抛物线C:y2=x的焦点,S是抛物线C在第一象限内的点,且|SF|=54.(1)求 2020-05-14 …
如图,在▱ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接B 2020-05-17 …
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥ 2020-05-17 …
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分 2020-05-17 …