通常我们把三条侧棱两两垂直的三棱锥称作“直角三棱锥”，在一次研究性学习活动中，老师组织同学们对“直角三棱锥”的性质进行了探究，已知直角三棱锥P-ABC中，PA，PB，PC两两垂直，

Question

通常我们把三条侧棱两两垂直的三棱锥称作“直角三棱锥”，在一次研究性学习活动中，老师组织同学们对“直角三棱锥”的性质进行了探究，已知直角三棱锥P-ABC中，PA，PB，PC两两垂直，且PA=a，PB=b，PC=c，下面的5个研究小组的研究成果：
①△ABC可能为钝角三角形；
②PA⊥BC；
③顶点P在底面ABC内的射影为△ABC的重心；
④三个侧面PAB，PAC，PBC两两垂直；
⑤该三棱锥的外接球的半径为 (1)/(2) √(a2+b2+c2)，
其中正确结论的序号为___．

Answer 1

直角三棱锥P-ABC中，PA，PB，PC两两垂直，且PA=a，PB=b，PC=c，
①△ABC可能是钝角三角形，P在底面是射影在△ABC的内部，是三角形ABC的垂心，所以不可能是钝角三角形，①不正确；
②PA⊥BC，由此条件可以得出，每一条棱都垂直于另外两条棱所确定的平面，由线面垂直即可即出PA⊥BC，故命题正确；
③P在底面是射影在△ABC的内部，由顶点P作三棱锥的高，其垂足是△ABC的垂心，由PA⊥BC，PB⊥AC，PC⊥AB，知三侧棱在底面的射影一定垂直于对边，故垂足是△ABC的垂心，③命题不正确；
④三个侧面PAB，PAC，PBC两两垂直，因为三条侧棱两两垂直，由直线与平面垂直的判定定理以及平面与平面垂直的判定定理可知，命题④是正确的；
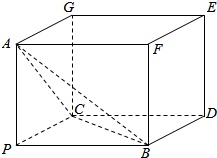⑤，以PA、PB、PC为过同一顶点的三条棱，作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为√(a2+b2+c2)，
∴球直径为：√(a2+b2+c2)，半径R=(1)/(2)√(a2+b2+c2)，
∴⑤正确；
故答案为：②④⑤．