早教吧作业答案频道 -->数学-->
在△ABC中,H为垂心,G为重心,O为外心,求证:.
题目详情
在△ABC中,H为垂心,G为重心,O为外心,求证: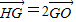 .
.
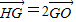 .
.▼优质解答
答案和解析
分析:
分析:
根据题意作出图形,由外心和垂心的性质证明四边形AHCD是平行四边形,由向量加法的三角形法则得 =+,由向量相等和向量的减法运算进行转化,得到 ,再根据△ABC重心为G满足 =,结合已知中 ,我们易判断出 =3 ,根据数乘向量的几何意义,即可得到O,G,H三点共线,且OG:GH=1:2即可.
如图:作直径BD,连接DA、DC,由图得,=-,∵H为△ABC的垂心,∴CH⊥AB,AH⊥BC,∵BD为直径,∴DA⊥AB,DC⊥BC∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,∴=又∵=-=+,∴=+=+=++,∵G为△ABC的重心∴=3 =3 +=即 =3 即O,G,H三点共线,且OH=3OG即O,G,H三点共线,且OG:GH=1:2.从而得到:.
点评:
点评:
本题考查的知识点是三角形的五心,其中熟练掌握向量五心的向量表达式形式,如(1)中△ABC外心为O满足 ,(2)中△ABC重心为G满足 =,是解答此类问题的关键.
分析:
分析:
根据题意作出图形,由外心和垂心的性质证明四边形AHCD是平行四边形,由向量加法的三角形法则得 =+,由向量相等和向量的减法运算进行转化,得到 ,再根据△ABC重心为G满足 =,结合已知中 ,我们易判断出 =3 ,根据数乘向量的几何意义,即可得到O,G,H三点共线,且OG:GH=1:2即可.
如图:作直径BD,连接DA、DC,由图得,=-,∵H为△ABC的垂心,∴CH⊥AB,AH⊥BC,∵BD为直径,∴DA⊥AB,DC⊥BC∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,∴=又∵=-=+,∴=+=+=++,∵G为△ABC的重心∴=3 =3 +=即 =3 即O,G,H三点共线,且OH=3OG即O,G,H三点共线,且OG:GH=1:2.从而得到:.
点评:
点评:
本题考查的知识点是三角形的五心,其中熟练掌握向量五心的向量表达式形式,如(1)中△ABC外心为O满足 ,(2)中△ABC重心为G满足 =,是解答此类问题的关键.
看了 在△ABC中,H为垂心,G为...的网友还看了以下:
在△ABC中,H为垂心,G为重心,O为外心,求证:. 2020-05-16 …
证明三角形外心与各点连线的向量和等于外心与垂心连线的向量O为外心,H为垂心,ABC为三角形三点 2020-05-16 …
已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM 2020-06-07 …
一.已知△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.延续上面(1)求证:A 2020-06-07 …
I为内心H为垂心O为外心若IH=IO求证ABC一个角为60度你给的是边边角证不到全等 2020-07-30 …
已知△ABC中,∠A=60°,H为垂心,O为外心,I是内心.求证:(1)AO=AH;(2)B、O、 2020-07-30 …
以O为外心,I为内心的三角形的三角形有几个?O,I为定点.以O为外心,I为内心的三角形有几个? 2020-07-30 …
已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM 2020-07-30 …
已知锐角△ABC中,AD是高,O是外心,AO的延长线交过O、B、C三点的圆于P,自P作PE⊥AB于 2020-07-30 …
一个三角形的问题…………已知三角形ABC内切圆,外接圆半径分别是r,R,求证:OI=R(R-2r) 2020-07-31 …